2127. Maximum Employees to Be Invited to a Meeting
A company is organizing a meeting and has a list of n employees, waiting to be invited. They have arranged for a large circular table, capable of seating any number of employees.
The employees are numbered from 0 to n - 1. Each employee has a favorite person and they will attend the meeting only if they can sit next to their favorite person at the table. The favorite person of an employee is not themself.
Given a 0-indexed integer array favorite, where favorite[i] denotes the favorite person of the ith employee, return the maximum number of employees that can be invited to the meeting.
Example 1:
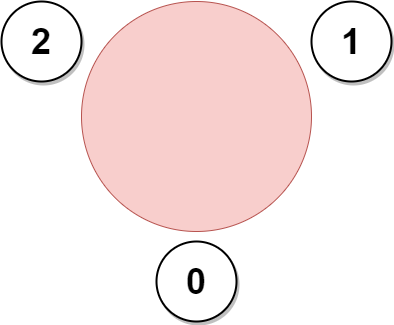
Input: favorite = [2,2,1,2] Output: 3 Explanation: The above figure shows how the company can invite employees 0, 1, and 2, and seat them at the round table. All employees cannot be invited because employee 2 cannot sit beside employees 0, 1, and 3, simultaneously. Note that the company can also invite employees 1, 2, and 3, and give them their desired seats. The maximum number of employees that can be invited to the meeting is 3.
Example 2:
Input: favorite = [1,2,0] Output: 3 Explanation: Each employee is the favorite person of at least one other employee, and the only way the company can invite them is if they invite every employee. The seating arrangement will be the same as that in the figure given in example 1: - Employee 0 will sit between employees 2 and 1. - Employee 1 will sit between employees 0 and 2. - Employee 2 will sit between employees 1 and 0. The maximum number of employees that can be invited to the meeting is 3.
Example 3:
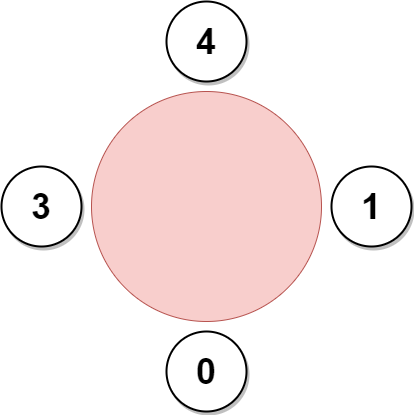
Input: favorite = [3,0,1,4,1] Output: 4 Explanation: The above figure shows how the company will invite employees 0, 1, 3, and 4, and seat them at the round table. Employee 2 cannot be invited because the two spots next to their favorite employee 0 are taken. So the company leaves them out of the meeting. The maximum number of employees that can be invited to the meeting is 4.
Constraints:
n == favorite.length2 <= n <= 1050 <= favorite[i] <= n - 1favorite[i] != i
JAVA
class Solution { public int maximumInvitations(int[] favorite) { return Math.max(maxCycle(favorite), topologicalSort(favorite)); } private int maxCycle(int[] fa) { int n = fa.length; boolean[] vis = new boolean[n]; int ans = 0; for (int i = 0; i < n; ++i) { if (vis[i]) { continue; } List<Integer> cycle = new ArrayList<>(); int j = i; while (!vis[j]) { cycle.add(j); vis[j] = true; j = fa[j]; } for (int k = 0; k < cycle.size(); ++k) { if (cycle.get(k) == j) { ans = Math.max(ans, cycle.size() - k); } } } return ans; } private int topologicalSort(int[] fa) { int n = fa.length; int[] indeg = new int[n]; int[] dist = new int[n]; Arrays.fill(dist, 1); for (int v : fa) { indeg[v]++; } Deque<Integer> q = new ArrayDeque<>(); for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { q.offer(i); } } int ans = 0; while (!q.isEmpty()) { int i = q.pollFirst(); dist[fa[i]] = Math.max(dist[fa[i]], dist[i] + 1); if (--indeg[fa[i]] == 0) { q.offer(fa[i]); } } for (int i = 0; i < n; ++i) { if (i == fa[fa[i]]) { ans += dist[i]; } } return ans; } }
C++
// Time: O(N)
// Space: O(N)
class Solution {
public:
int maximumInvitations(vector<int>& A) {
int N = A.size();
vector<int> m(N, -1); // m[i] is the depth of node i. -1 means unvisited
vector<vector<int>> r(N); // The reverse graph
for (int i = 0; i < N; ++i) r[A[i]].push_back(i);
// handle case 1
function<int(int)> dfs = [&](int u) {
if (m[u] != -1) return m[u];
int ans = 0;
for (int v : r[u]) ans = max(ans, dfs(v));
return m[u] = 1 + ans;
};
int ans = 0, free = 0;
for (int i = 0; i < N; ++i) {
if (m[i] != -1) continue; // skip visited nodes
if (A[A[i]] == i) {
m[i] = m[A[i]] = 0;
int a = 0, b = 0; // find the length of the longest arms starting from `i` and `A[i]`
for (int v : r[i]) {
if (v == A[i]) continue;
a = max(a, dfs(v));
}
for (int v : r[A[i]]) {
if (v == i) continue;
b = max(b, dfs(v));
}
free += a + b + 2; // this free component is of length `a+b+2`
}
}
// handle case 2
function<tuple<int, int, bool>(int)> dfs2 = [&](int u)->tuple<int, int, bool> {
if (m[u] != -1) return {u, m[u], false}; // We visited this node the second time, so this node must be the entry point to the cycle
m[u] = 0;
auto [entryPoint, depth, cycleVisited] = dfs2(A[u]);
if (cycleVisited) { // After the cycle being traversed, any other node in the backtracking process are outside of the cycle and should be ignored (by keeping m[u] as 0).
return {entryPoint, depth, true};
}
m[u] = 1 + depth; // If we haven't met the entry point again, this is a node within the cycle, so we increment the depth.
return {entryPoint, m[u], u == entryPoint}; // When we visit the entry point again, we know what we've done traversing the cycle.
};
for (int i = 0; i < N; ++i) {
if(m[i] != -1) continue;
auto [entryPoint, depth, cycleVisited] = dfs2(i);
if (cycleVisited) ans = max(ans, depth);
}
return max(ans, free);
}
};PYTHON
from collections import deque class Solution: def maximumInvitations(self, favorite): def max_cycle(fa): n = len(fa) vis = [False] * n ans = 0 for i in range(n): if vis[i]: continue cycle = [] j = i while not vis[j]: cycle.append(j) vis[j] = True j = fa[j] for k in range(len(cycle)): if cycle[k] == j: ans = max(ans, len(cycle) - k) return ans def topological_sort(fa): n = len(fa) indeg = [0] * n dist = [1] * n for v in fa: indeg[v] += 1 q = deque() for i in range(n): if indeg[i] == 0: q.append(i) ans = 0 while q: i = q.popleft() dist[fa[i]] = max(dist[fa[i]], dist[i] + 1) indeg[fa[i]] -= 1 if indeg[fa[i]] == 0: q.append(fa[i]) for i in range(n): if i == fa[fa[i]]: ans += dist[i] return ans return max(max_cycle(favorite), topological_sort(favorite))
Comments
Post a Comment