2684. Maximum Number of Moves in a Grid

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

 Example 1:

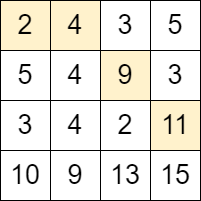
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
Output: 3
Explanation: We can start at the cell (0, 0) and make the following moves:
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
It can be shown that it is the maximum number of moves that can be made.

Example 2:

Input: grid = [[3,2,4],[2,1,9],[1,1,7]]
Output: 0
Explanation: Starting from any cell in the first column we cannot perform any moves.

 Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

C++

• class Solution {
  public:
      int maxMoves(vector<vector<int>>& grid) {
          int m = grid.size(), n = grid[0].size();
          int dist[m][n];
          memset(dist, 0, sizeof(dist));
          int ans = 0;
          queue<pair<int, int>> q;
          for (int i = 0; i < m; ++i) {
              q.emplace(i, 0);
          }
          int dirs[3][2] = { {-1, 1}, {0, 1}, {1, 1} };
          while (!q.empty()) {
              auto [i, j] = q.front();
              q.pop();
              for (int k = 0; k < 3; ++k) {
                  int x = i + dirs[k][0], y = j + dirs[k][1];
                  if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > grid[i][j] && dist[x][y] < dist[i][j] + 1) {
                      dist[x][y] = dist[i][j] + 1;
                      ans = max(ans, dist[x][y]);
                      q.emplace(x, y);
                  }
              }
          }
          return ans;
      }
  };

JAVA

• class Solution {
      public int maxMoves(int[][] grid) {
          int[][] dirs = { {-1, 1}, {0, 1}, {1, 1} };
          int m = grid.length, n = grid[0].length;
          Deque<int[]> q = new ArrayDeque<>();
          for (int i = 0; i < m; ++i) {
              q.offer(new int[] {i, 0});
          }
          int[][] dist = new int[m][n];
          int ans = 0;
          while (!q.isEmpty()) {
              var p = q.poll();
              int i = p[0], j = p[1];
              for (var dir : dirs) {
                  int x = i + dir[0], y = j + dir[1];
                  if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] > grid[i][j]
                      && dist[x][y] < dist[i][j] + 1) {
                      dist[x][y] = dist[i][j] + 1;
                      ans = Math.max(ans, dist[x][y]);
                      q.offer(new int[] {x, y});
                  }
              }
          }
          return ans;
      }
  }

PYTHON

• from collections import deque
  
  class Solution:
      def maxMoves(self, grid):
          m, n = len(grid), len(grid[0])
          dist = [[0] * n for _ in range(m)]
          ans = 0
          q = deque([(i, 0) for i in range(m)])
          
          dirs = [(-1, 1), (0, 1), (1, 1)]
          
          while q:
              i, j = q.popleft()
              for dx, dy in dirs:
                  x, y = i + dx, j + dy
                  if 0 <= x < m and 0 <= y < n and grid[x][y] > grid[i][j] and dist[x][y] < dist[i][j] + 1:
                      dist[x][y] = dist[i][j] + 1
                      ans = max(ans, dist[x][y])
                      q.append((x, y))
          
          return ans