2458. Height of Binary Tree After Subtree Removal Queries

You are given the root of a binary tree with n nodes. Each node is assigned a unique value from 1 to n. You are also given an array queries of size m.

You have to perform m independent queries on the tree where in the ith query you do the following:

• Remove the subtree rooted at the node with the value queries[i] from the tree. It is guaranteed that queries[i] will not be equal to the value of the root.

Return an array **answer of size m where answer[i] is the height of the tree after performing the ith query**.

Note:

• The queries are independent, so the tree returns to its initial state after each query.

• The height of a tree is the number of edges in the longest simple path from the root to some node in the tree.

  Example 1:

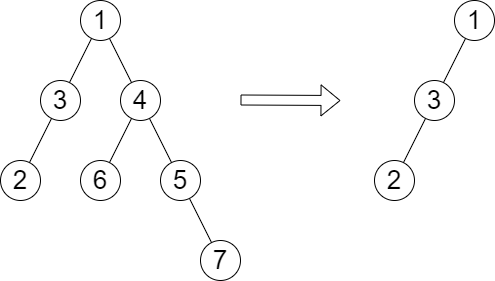
Input: root = [1,3,4,2,null,6,5,null,null,null,null,null,7], queries = [4]
Output: [2]
Explanation: The diagram above shows the tree after removing the subtree rooted at node with value 4.
The height of the tree is 2 (The path 1 -> 3 -> 2).

Example 2:

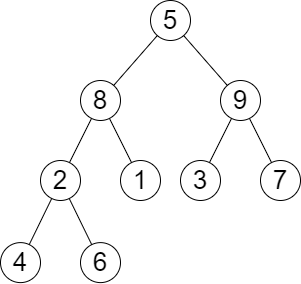
Input: root = [5,8,9,2,1,3,7,4,6], queries = [3,2,4,8]
Output: [3,2,3,2]
Explanation: We have the following queries:
- Removing the subtree rooted at node with value 3. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 4).
- Removing the subtree rooted at node with value 2. The height of the tree becomes 2 (The path 5 -> 8 -> 1).
- Removing the subtree rooted at node with value 4. The height of the tree becomes 3 (The path 5 -> 8 -> 2 -> 6).
- Removing the subtree rooted at node with value 8. The height of the tree becomes 2 (The path 5 -> 9 -> 3).

  Constraints:

• The number of nodes in the tree is n.

• 2 <= n <= 105

• 1 <= Node.val <= n

• All the values in the tree are unique.

• m == queries.length

• 1 <= m <= min(n, 104)

• 1 <= queries[i] <= n

• queries[i] != root.val

C++

class Solution {
public:
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        unordered_map<TreeNode*, int> d;
        function<int(TreeNode*)> f = [&](TreeNode* root) -> int {
            if (!root) return 0;
            int l = f(root->left), r = f(root->right);
            d[root] = 1 + max(l, r);
            return d[root];
        };
        f(root);
        vector<int> res(d.size() + 1);
        function<void(TreeNode*, int, int)> dfs = [&](TreeNode* root, int depth, int rest) {
            if (!root) return;
            ++depth;
            res[root->val] = rest;
            dfs(root->left, depth, max(rest, depth + d[root->right]));
            dfs(root->right, depth, max(rest, depth + d[root->left]));
        };
        dfs(root, -1, 0);
        vector<int> ans;
        for (int v : queries) ans.emplace_back(res[v]);
        return ans;
    }
};

JAVA

class Solution {
    private Map<TreeNode, Integer> d = new HashMap<>();
    private int[] res;

    public int[] treeQueries(TreeNode root, int[] queries) {
        f(root);
        res = new int[d.size() + 1];
        d.put(null, 0);
        dfs(root, -1, 0);
        int m = queries.length;
        int[] ans = new int[m];
        for (int i = 0; i < m; ++i) {
            ans[i] = res[queries[i]];
        }
        return ans;
    }

    private void dfs(TreeNode root, int depth, int rest) {
        if (root == null) {
            return;
        }
        ++depth;
        res[root.val] = rest;
        dfs(root.left, depth, Math.max(rest, depth + d.get(root.right)));
        dfs(root.right, depth, Math.max(rest, depth + d.get(root.left)));
    }

    private int f(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int l = f(root.left), r = f(root.right);
        d.put(root, 1 + Math.max(l, r));
        return d.get(root);
    }
}

PYTHON

from typing import List, Optional

# Definition for a binary tree node.
class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def treeQueries(self, root: Optional[TreeNode], queries: List[int]) -> List[int]:
        d = {}
        
        def f(node: Optional[TreeNode]) -> int:
            if not node:
                return 0
            left_depth = f(node.left)
            right_depth = f(node.right)
            d[node] = 1 + max(left_depth, right_depth)
            return d[node]
        
        f(root)
        
        res = [0] * (len(d) + 1)
        
        def dfs(node: Optional[TreeNode], depth: int, rest: int):
            if not node:
                return
            depth += 1
            res[node.val] = rest
            dfs(node.left, depth, max(rest, depth + d.get(node.right, 0)))
            dfs(node.right, depth, max(rest, depth + d.get(node.left, 0)))
        
        dfs(root, -1, 0)
        
        return [res[q] for q in queries]